In diesem Abschnitt wird eine neue Methode zur Bestimmung einer Abstiegsrichtung vorgestellt, die auf lokalen Verschiebungen von Belastungen basiert, welche die Gesamtkosten verringern und die leicht berechenbaren Informationen ausnutzen, die durch die Ableitungen der Kantenkosten nach den Kantenbelastungen zur Verfügung stehen.
Die grundlegende Idee wird sofort klar, wenn sie am Beispiel des einfachsten Netzes erklärt wird, in dem eine einzige QZ-Beziehung mit der Nachfrage D durch zwei Kanten mit der Kostenfunktion c1(f1) bzw. c2(f2) verbunden ist. Bei der aktuellen Belastung f′ = (D/2, D/2) ist dies c1′ < c2 (siehe Abbildung 100), sodass ein Alles-oder-Nichts-Ansatz zu einer Abstiegsrichtung (D, 0) führen würde, die weit entfernt ist vom Gleichgewicht f* (grauer Kreis in der Abbildung). Der LUCE-Ansatz berücksichtigt stattdessen die Näherungen erster Ordnung der Kostenfunktionen an den aktuellen Belastungen, d.h. ca′ + ∂ ca(fa)/∂ fa• (fa - fa′) und ermittelt ein Nutzergleichgewicht e über diese Linien (weißer Kreis in der Abbildung): Diese Abstiegsrichtung nähert sich dem Gleichgewicht f* sehr schnell. In den meisten Fällen kann sogar die maximale Schrittweite a=1 verwendet werden.
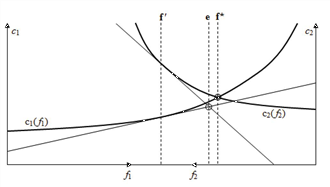
Abbildung 100: Linear User Cost Equilibrium zwischen zwei Wegen
Um ein Ziel d∈Z zu erreichen, werden im Gleichgewicht nur Kurzwege genutzt. Da die Kantenkostenfunktionen streng monoton steigend sind, bilden sie einen azyklischen Teilgraph von G, d.h. einen (umgekehrten) Busch, der an d verwurzelt ist. Bei strenger Monotonie können Kantenkosten tatsächlich nur null sein, wenn auch die Belastung null ist. In Visum können Strecken und Anbindungen jedoch auch bei positiver Belastung einen Widerstand von null haben, was zweifache Konsequenzen hat: a) Die zugehörigen Kantenkostenfunktionen verlieren die strenge Monotonie, sodass die Eindeutigkeit nicht mehr garantiert ist. b) Der Teilgraph, der aus Kanten mit positiven Zielbelastungen an einigen möglichen Gleichgewichten besteht, kann zyklisch sein. Die Implementierung von LUCE in Visum behandelt dieses Problem gezielt und konvergiert in eins der möglichen Gleichgewichte, indem es eine azyklische Lösung erzwingt und die Belastung in solchen Fällen unter allen Alternativen mit minimalen Kosten im unbelasteten Netz aufteilt. Wir gehen auf diesen Sonderfall in der nachfolgenden Beschreibung nicht mehr besonders ein.
Suchen wir auf dieser Grundlage nach einer Abstiegsrichtung, konzentrieren wir uns im Folgenden auf den aktuellen Busch B(d) und führen einen Aktualisierungsmechanismus ein, um sicherzustellen, dass letztendlich jeder Kurzweg darin enthalten ist; nur auf diese Weise wird das Gleichgewicht wirklich erreicht. Wir betrachten die lokale Routenwahl an einem generischen Knoten i∈N für Verkehrsteilnehmer, die das Ziel d∈Z anfahren.
Für die Topologie des Busches nutzen wir folgende Schreibweise:
|
FSB(i, d) = {j∈N: ij∈B(d)} |
diejenigen Knoten, die von Knoten i∈N über Kanten des aktuellen Buschs B(d) zu Ziel d∈Z erreicht werden (Forward Star) |
|
BSB(i, d) = {j∈N: ij∈B(d)} |
diejenigen Knoten, von denen aus Knoten i∈N über Kanten des aktuellen Buschs B(d) zu Ziel d∈Z erreicht werden (Backward Star) |
Für die Belastungen wird folgende Schreibweise verwendet:
|
fijd |
aktuelle Belastung auf Kante ij∈A zum Ziel d∈Z Durch Konstruktion gilt fijd= 0 für jedes j∉FSB(i, d); außerdem gilt eindeutig: fij=∑d∈Zfijd |
|
fid = ∑j∈FSB(i, d)fijd |
aktuelle Belastung von Knoten i∈N zum Ziel d∈Z |
|
yijd |
yijd = fijd / fidaktueller Belastungsanteil auf Kante ij∈A zum Ziel d∈Z, wenn fid > 0, yijd = 0 andernfalls |
|
eijd |
Abstiegsrichtung hinsichtlich der Belastung auf Kante ij∈A zum Ziel d∈Z |
|
eid |
Abstiegsrichtung hinsichtlich der Belastung von Knoten i∈N zum Ziel d∈Z |
|
eijd = eijd / eid |
Abstiegsrichtung ausgedrückt als Belastungsanteil auf Kante ij∈A zum Ziel d∈Z |
Für das Kostenmuster wird folgende Schreibweise verwendet:
|
Cid |
durchschnittliche Kosten, um Ziel d∈Z von Knoten i∈N zu erreichen |
|
gij |
Kostenableitung der Kante ij∈A |
|
Gid |
Ableitung der durchschnittlichen Kosten, um Ziel d∈Z von Knoten i∈N zu erreichen |
Die durchschnittlichen Kosten Cid stellen den erwarteten Widerstand dar, auf den ein Verkehrsteilnehmer stößt, wenn er sich von Knoten i∈N zum Ziel d∈N bewegt. Hier werden sie, basierend auf den aktuellen Belastungen, rekursiv definiert:
falls fid > 0, dann Cid = ∑j∈FSB(i, d)yijd • (cij + Cjd), sonst [16.1]
Cid = min{cij + Cjd: j∈FSB(i, d)}, [16.2]
als ob Fahrer Wege entsprechend den aktuellen Belastungsanteilen nutzen. Im Folgenden gehen wir davon aus, dass die Kostenfunktion cij(fij) für jede Kante ij∈A kontinuierlich differenzierbar ist:
gij = ∂cij(fij) / ∂fij [17]
In der Annahme, dass ein infinitesimales Inkrement der Belastung von Knoten i∈N zum Ziel d∈Z sich entsprechend den aktuellen Abbiegeranteilen unter den ausgehenden Kanten aufteilen würde, ergibt sich:
falls fid > 0, dann Gid = ∂Cid / ∂fid = ∑j∈FSB(i, d)yijd2• (gij + Gjd), sonst [18.1]
Gid = ∑j∈FSB(i, d) [Cid = cij + Cjd] • (gij + Gjd) / ∑j∈FSB(i, d) [Cid = cij + Cjd], [18.2]
wobei die Ableitungen gij + Gjd mit dem Anteil yijd von ∂fid skaliert werden, der erst Kante ij und danach Knoten j durchfährt, was zusammen mit dem an der Mittelung beteiligten Belastungsanteil die zweite Potenz yijd2 ergibt.
Die durchschnittlichen Kosten und ihre Ableitungen können berechnet werden, indem die Knoten des Buschs in umgekehrter topologischer Reihenfolge (in der Reihenfolge aufsteigender Kosten nach d) bearbeitet werden, beginnend mit Cdd = Gdd = 0.
Betrachten wir nun das lokale Nutzergleichgewicht für die Fahrer eid zum Ziel d∈Z, deren nutzbare Alternativen die Kanten des von Knoten i∈N ausgehenden Buschs sind. Jeder Alternative ordnen wir folgende Kostenfunktion zu:
vijd(eijd) = (cij + Cjd) + (gij + Gjd) • (eijd - yijd • eid), [19]
resultierend aus einer Linearisierung an den aktuellen Belastungen der durchschnittlichen Kosten eines Verkehrsteilnehmers, der die Kante ij nutzt, mit j∈FSB(i, d).
Analog zu [10.1] bis [10.4] kann dieses Problem durch das folgende System von Ungleichungen ausgedrückt werden:
eijd • [vijd(eijd) - Vid] = 0, ∀j∈FSB(i, d), [20.1]
vijd(eijd) ≥ Vid, ∀j∈FSB(i, d), [20.2]
eijd≥0, ∀j∈FSB(i, d), [20.3]
∑j∈FSB(i, d)eijd = eid, [20.4]
wobei gilt:
|
Vid |
lokale Gleichgewichtskosten, um das Ziel d∈Z von Knoten i∈N zu erreichen; |
|
vijd |
Kosten der lokalen Alternative j∈FSB(i, d), um das Ziel d∈Z von Knoten i∈N via j zu erreichen. |
Wenn eid = 0, ist die triviale Lösung für das obige Problem: eijd = 0, für jedes j∈FSB(i, d). Betrachten wir nun den Fall, in dem eid > 0. Um die Lesbarkeit zu erleichtern, nehmen wir in [20.1] bis [20.4] folgende Umbenennungen vor:
xj • (aj + bj • xj - v) = 0, ∀j∈J, [21.1]
wobei:
|
J |
{(i, j, d): j∈FSB(i, d)} |
|
aj |
(cij + Cjd) - (gij + Gjd) • eid • yijd |
|
bj |
(gij + Gjd) • eid |
|
xj |
eijd / eid |
|
v |
Vid |
Wird der übliche Beckmann-Ansatz angewandt, können wir das Gleichgewichtsproblem [21.1] bis [21.4] wie folgt als quadratisches Programm neu formulieren:
min{∑j∈J 0òxj(aj + bj • x) • dx: x∈X} = min{∑j∈Jaj • xj + 0.5 • bj • xj2: x∈X}, [22]
wobei X die konvexe Menge aller Vektoren darstellt, die die Bedingungen [21.3] und [21.4] erfüllen. Der Gradient der Zielfunktion ist ein Vektor mit dem generischen Element aj + bj • xj und die Hessematrix der Zielfunktion eine diagonale Matrix mit dem generischen Element bj. Sind also alle Elemente bj streng positiv, ist die Hessematrix positiv definit und das Problem [22] hat eine eindeutige Lösung. Um solch eine erwünschte Eigenschaft zu garantieren, gehen wir davon aus, dass die Ableitungen gij ohne Verlust der Allgemeingültigkeit für alle Kanten ij∈A streng positiv sind. Da die Kantenkostenfunktionen streng monoton steigend sind, kann gij nur null sein, wenn auch fijd null ist. Bei dem Gleichgewicht bj = 0 bedeutet das xj = 0. In der Praxis ersetzen wir jedes gij = 0 durch ein kleines ε.
Um das Problem [21.1] bis [21.4] zu lösen, benutzen wir folgende Methode. Um Bedingung [21.1] zu erfüllen, gilt entweder xj = 0 (und in diesem Fall erfordert die Bedingung [21.2]aj ≥ v) oder es gilt aj + bj • xj = v. Sei J0 ⊂ J die Menge der Alternativen ohne Belastung, dann ist J0 = {j∈J: xj = 0}. Bei gegebenem J0 ist die Lösung sofort klar, weil basierend auf [21.4]∑j∈J (v - aj) / bj = 1 gilt; daher gilt:
v = (1 + ∑j∈J\J0aj / bj) / (∑j∈J\J0 1 / bj), [23.1]
xj = (v - aj) / bj, ∀j∈J\J0, [23.2]
Die durch [23.1] bis [23.3] gegebenen Belastungsanteile erfüllen [21.4] implizit. Damit aber das ausgewählte J0 die Lösung von Problem [21.1] bis [21.4] liefert, müssen außerdem folgende Bedingungen gewährleistet sein: aj < v, für jedes j∈J\J0 (wie durch [21.3] vorgeschrieben, da xj = (v - aj) / bj > 0), und aj ≥ v, für jedes j∈J0 (wie durch [21.2] vorgeschrieben, da xj = 0). Das setzt voraus, dass bei der Lösung des Wertes v, der aus [23.1] resultiert, die Menge J in zwei Teilmengen unterteilt wird: die Menge J0, die sich aus den Alternativen j ergibt, sodass aj ≥ v, und ihrem Komplement J\J0, das sich aus den Alternativen j ergibt, sodass aj < v.
Zunächst mag das Problem, die Menge J0 zu bestimmen, kombinatorisch erscheinen. Dies ist jedoch nicht der Fall. Die Gleichung [23.1] kann als rekursive Formel umschrieben werden. Sie zeigt dann die Auswirkung des Entfernens einer Alternative k aus der Menge J0:
v[J0\{k}] = (v[J0] • ∑j∈J\J0 1 / bj + ak / bk) / (∑j∈J\J0 1 / bj + 1 / bk) . [24]
Die rechte Seite von [24] kann als Mittelwert zwischen v[J0] und ak interpretiert werden mit den positiven Gewichten ∑j∈J\J0 1 / bj und 1 / bk. Die lokalen Nutzergleichgewichtskosten nehmen daher zu, wenn aus J0 irgendwelche Alternativen k∈J\J0, für die ak höher ist als der aktuelle Wert v[J0], entfernt werden. Umgekehrt nehmen sie ab, wenn solche Alternativen zu J0 hinzugefügt werden. Folglich ergibt sich die korrekte Teilmenge J0 einfach, indem jede Alternative j∈J\J0 iterativ zur anfangs leeren Menge hinzugefügt wird, sodass aj > v, d.h. jede Alternative, für die [23.2] einen negativen Belastungsanteil erzielt.

